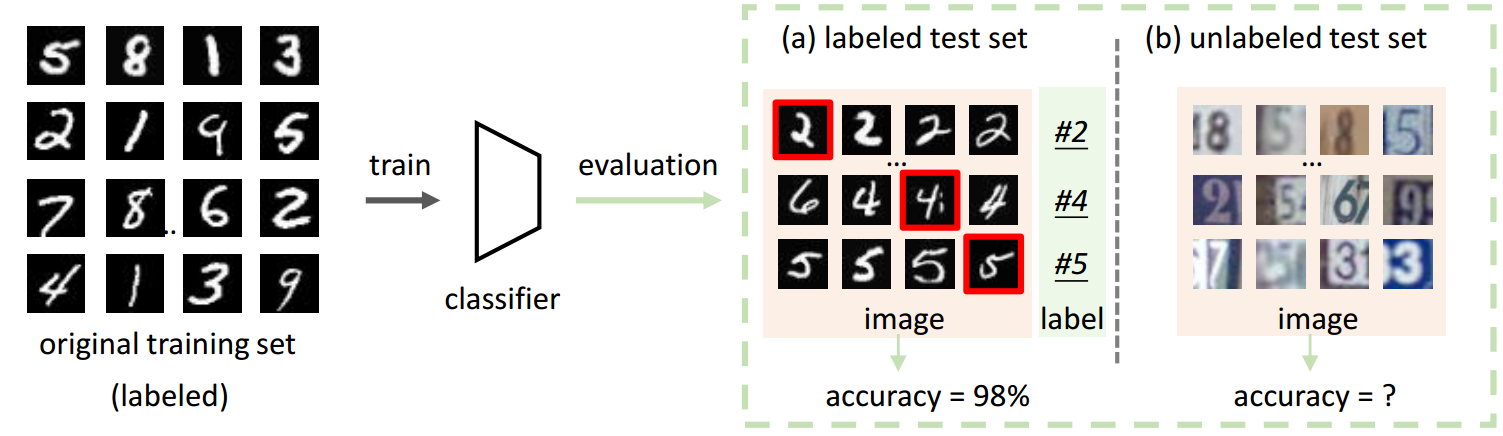
Automatic Model Evaluation Understanding Model Decision under Dynamic Testing Environments. Given a classifier trained on a training set, we can gain a hopefully unbiased estimate of its real world performance by evaluating it on an unseen labeled test dataset, as shown in (a). However, in many real-world deployment scenarios, we are presented with unlabeled test datasets (b), and as such are unable to evaluate our classifier using common metrics. This inspired us to explore the problem of Automatic model Evaluation.

To calculate the model accuracy on a computer vision task, e.g., object recognition, we usually require a test set composing of test samples and their ground truth labels. Whilst standard usage cases satisfy this requirement, many real world scenarios involve unlabeled test data, rendering common model evaluation methods infeasible. We investigate this important and under-explored problem, Automatic model Evaluation (AutoEval) . Specifically, given a labeled training set and a classifier, we aim to estimate the classification accuracy on unlabeled test datasets. We construct a meta-dataset: a dataset comprised of datasets generated from the original images via various transformations such as rotation, background substitution, foreground scaling, etc. As the classification accuracy of the model on each sample (dataset) is known from the original dataset labels, our task can be solved via regression. Using the feature statistics to represent the distribution of a sample dataset, we can train regression techniques (e.g., a regression neural network) to predict model performance. Using synthetic meta-dataset and real-world datasets in training and testing, respectively, we report reasonable and promising predictions of the model accuracy. We also provide insights into the application scope, limitation, and potential future directions of AutoEval.

A. Motivation. Motivated by the implications (distribution shift affects classifier accuracy) in domain adaptation, we propose to address AutoEval by measuring the distribution difference between the original training set and the test set, and explicitly learning a mapping function from the distribution shift to the classifier accuracy.

B. Meta Dataset. We study the relationship between distribution shift and classifier accuracy. To this end, we construct a meta dataset (dataset of datasets). To construct such a meta set, we should collect sample sets that are 1) large in number, 2) diverse in the data distribution, and 3) have the same label space as the original training set. There are very few real-world datasets that satisfy these requirements, so we resort to data synthesis.

Given a seed set, we use image transformations (e.g., rotation, autoContrast, translation) and background change for its images. Using different transformations and backgrounds, we can generate many diverse sample sets. Seed set and examples of fifteen sample sets are shown below. The seed set is sampled from the same distribution as the original training set; they share the same classes but do not have image overlap. The sample sets are generated from the seed by background replacement and image transformations. The sample sets exhibit distinct data distributions, but inherit the foreground objects from the seed, and hence are fully labeled.

C. Correlation. Given a classifer (trained on training set D_ori) and a meta dataset, we show the accuracy as a function of the distribution shift. The distribution shift is measured by Frechet distance (FD) with the features extracted from the trained classifier. In practice, we use the activations in the penultimate of the classifier as features. For each sample set, we calculate the FD between it and training set D_ori, and classifier accuracy on it. In the following figure, we observe that there is a strong linear correlation between classifier accuracy and distribution shift. This observation is consistent across three different classifiers. This validates the feasibility of estimating classifier accuracy from dataset-level feature statistics.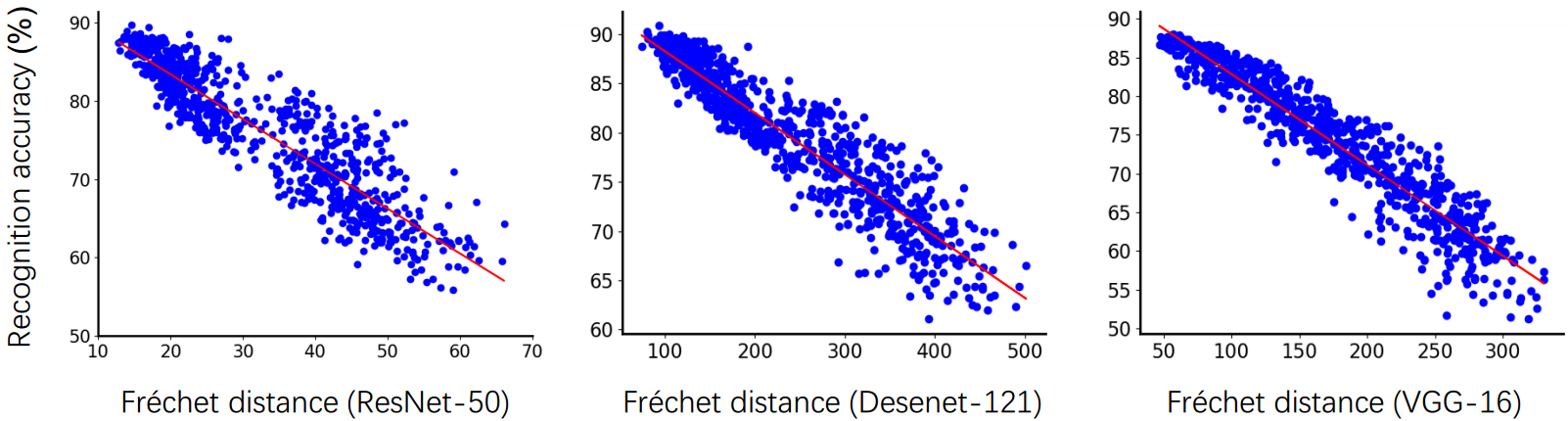

D. Learning to estimate. With the above correlation, we could predict classifier accuracy on an unseen test set based on its distribution shift between training set. In this paper, we propose two regression methods:

• linear regression: For each sample set from meta dataset, we calculate classifier accuracy and its distribution shift (FD) between training set D_ori. Then, we can learn a simple linear regression, which takes as input FD and returns estimated accuracy.
• network regression: We use distribution-related statistics to represent each sample set. In practice, we use its first-order and second-order feature statistics, i.e., mean vector and covariance matrix. Then, we build up a small fully-connected network to learn the mapping function: the network uses the mean vector and covariance matrix of a sample set as input and outputs estimated accuracy. In this way, the network learns to predict classifier accuracy on an unseen test set using its mean vector and covariance matrix

Note that, we learn the above two regression methods on meta dataset, and test them on unseen real-world test sets (Caltech, Pascal, and ImageNet). The experimental results show that our methods make promising and reasonable predictions (the RMSE is less than 4%). This is because our meta dataset contains many diverse sample sets, such that regression methods "see" various cases. In this paper, we provide experiments to validate the robustness of regression and the crucial factors of the meta dataset. For more details, please check our paper.

This paper investigates the problem of predicting classifier accuracy on test sets without ground truth labels. It has the potential to yield significant practical value, such as predicting system failure in unseen real-world environments. Importantly, this task requires us to derive similarities and representations on the dataset level, which is significantly different from common image-level problems. We make some initial attempts by devising two regression models which directly estimate classifier accuracy based on overall distribution statistics. We build a dataset of datasets (meta-dataset) to train the regression model. We show that the synthetic meta-dataset can cover a good range of dataset distributions and benefit AutoEval on real-world test sets. For the remainder of this section, we discuss the limitations, potential, and interesting aspects of AutoEval.